飛谷ユミ子先生に誘われて「胎内記憶」の共著者である七田眞先生のドキュメンタリー映画『魂の教育』を見てきた。
七田先生のことを話すとき、時々疑似科学ではないかと言われる。疑似科学自体どのようなものであるか意見が分かれるところだが、確かに七田先生の話には科学的ではない部分がある。それは再現性のないことであったり、科学的な証明ができないことであったり、いろいろである。それを知った上でも七田先生には聞くべき話しがたくさんある。そのひとつは「信じることとはどのようなことか」についてだと僕は考えている。あることを信じることで生まれる心持ちがある。それが人を動かすことがある。それは科学的でなくてもいいような気が僕にはするのだ。
この映画の中で七田先生がかつて大病をしたという下りがある。肺炎だったのだが、医者にあと数ヶ月の命だろうと両親に伝えられる。それを若い七田先生が聞いてしまうのだ。そこで彼は死んでなるものかと起きあがり、無理をして運動する。そのうちに気力で治してしまったという。科学的に考えればあり得ない話しだが、現実としてはあり得るだろう。僕の父も黄疸になり、手術しないと間違いなく死ぬと言われたが、あくまでも手術は拒否して薬と食生活だけで治してしまった。
この映画で七田先生は若い頃に三つの危機が訪れるのではないかと漠然と思っていたことが語られる。ひとつは「死ぬほどの大病をする」。二つめは「貧乏をする」。そして「人に裏切られる」。その通りになることが再現ドラマで伝えられるが、どの体験を通しても七田先生はそれをポジティブに受け止める。
この映画を観たあとでたまたま「チベット密教 心の修行」という本を読んだ。以前チベット僧であるバリー博士の講演会に参加したのだが、そこで話題になっていた「ロジョン(心の訓練)」を和訳したものだ。そのなかに心の修行は五つの力によっておこなえと言う部分がある。
1.決意の力 修行するという決意を固めることのよって得られる。
2.慣れる力 修行を習慣にすることで得られる。
3.善根の力 修行は他人を思いやることによってできることを知ることで得られる。
4.対治の力 自己愛着をなくすことで得られる。
5.回向の力 修行によって得られる功徳をすべての人のために捧げるように祈ることで得られる。
この五つの力を七田先生は三つの危機を体験することで得ていったのだなと思った。まずは三つの危機が訪れてもひるまない自分になると決意する。賃金をきちんと払ってくれない会社に勤めていても、約束通りに働いたという話しが映画で紹介されるが、その体験が慣れる力と善根の力を生み出した。三つの危機を体験する覚悟をすることで自己愛着を手放し、対治の力を得た。そして、それらの体験を通して得られた気づきを幼児教育に生かすことで生きていこうと決めたことで回向の力を得たのである。
七田先生と同じような体験をしても、同じようにすべての人が考えるわけではないだろう。つまり、「大病をし」「貧乏し」「人に裏切られ」ても、必ずしもすべての人が幼児教育を始めるわけではない。人の人生に再現性はないのだ。つまり、人生を科学的に考えても意味がない。一回しかない人生であり、私にしか許されてない人生であり、私にしか与えられていない環境だから尊いのである。それが事実かどうかは科学では証明されない。そうであると信じる者にだけ、それが見える。

 よくやり玉に挙げられることのひとつが「水の結晶」だ。江本勝さんが「水からの伝言」という本にまとめたこと。水の入った器に言葉を書いたり、言葉の書かれた紙の上に水を置いておくと、言葉の質や内容によって、冷凍してできる結晶の形が異なるという内容だ。これが事実か否か、僕にはよくわからない。普通に考えれば、あり得ない話しだ。だけど実際に実験して確かめたわけでもないのでなんとも言えない。本当なら面白いし、嘘なら馬鹿げたことするなと思うし、ファンタジーなら素敵な想像力を持っているなということだ。今回その実験を見せてもらえることになった。しかも、世界賢人会議「ブダペストクラブ」の創設者、アーヴィン・ラズロ博士と一緒に。 ラズロ博士に会うために最近出版されたばかりの「CosMos」を読んでいった。
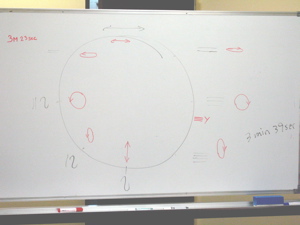
よくやり玉に挙げられることのひとつが「水の結晶」だ。江本勝さんが「水からの伝言」という本にまとめたこと。水の入った器に言葉を書いたり、言葉の書かれた紙の上に水を置いておくと、言葉の質や内容によって、冷凍してできる結晶の形が異なるという内容だ。これが事実か否か、僕にはよくわからない。普通に考えれば、あり得ない話しだ。だけど実際に実験して確かめたわけでもないのでなんとも言えない。本当なら面白いし、嘘なら馬鹿げたことするなと思うし、ファンタジーなら素敵な想像力を持っているなということだ。今回その実験を見せてもらえることになった。しかも、世界賢人会議「ブダペストクラブ」の創設者、アーヴィン・ラズロ博士と一緒に。 ラズロ博士に会うために最近出版されたばかりの「CosMos」を読んでいった。 しばらくしてラズロ博士がいらした。ラズロ博士はシャギ博士というヒーラーを連れてきた。シャギ博士はダウジングを使って人の状態を診る。「誰かからだの調子の悪い人はいませんか?」と言われ、「最近糖尿病だと言われ、薬を飲んでます」と答えたら、診てくれることになった。シャギ博士は僕の背中や頭に手をかざしてダウジングの振れを見る。するとその状態を見て僕の左手の人差し指の先と、小指の付け根に何か印のような物を書いてくれた。ダウジングの振り子の振れ方で印が決まるそうだ。ホワイトボードに右下の写真のように図を描いた。振り子が左右に振れるときは横に一本の線、右回りに平たく振れるときは二本の線、右回りに円のように振れるときは三本の線、縦長に右回りの楕円を描くときには四本の線を描くのだそうだ。
しばらくしてラズロ博士がいらした。ラズロ博士はシャギ博士というヒーラーを連れてきた。シャギ博士はダウジングを使って人の状態を診る。「誰かからだの調子の悪い人はいませんか?」と言われ、「最近糖尿病だと言われ、薬を飲んでます」と答えたら、診てくれることになった。シャギ博士は僕の背中や頭に手をかざしてダウジングの振れを見る。するとその状態を見て僕の左手の人差し指の先と、小指の付け根に何か印のような物を書いてくれた。ダウジングの振り子の振れ方で印が決まるそうだ。ホワイトボードに右下の写真のように図を描いた。振り子が左右に振れるときは横に一本の線、右回りに平たく振れるときは二本の線、右回りに円のように振れるときは三本の線、縦長に右回りの楕円を描くときには四本の線を描くのだそうだ。